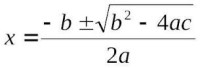1. 인수분해
- 인수 : 하나의 다항식을 두 개 이상의 다항식의 곱으로 나타낼 때의 각각의 식
- 인수분해 : 하나의 다항식을 두 개 이상의 다항식의 곱으로 나타내는 것
2. 공통인수를 이용한 인수분해
- 공통인수 : 다항식의 각 항에 공통으로 곱해져 있는 인수
- 공통인수를 이용한 인수분해 : 다항식의 각 항에 공통인수가 있을 때는 분배법칙을 이용하여 공통인수로 묶어 인수분해
3. 인수분해 공식
- 완전제곱식 : 다항식의 제곱으로 된 식 또는 이 식에 상수를 곱한 식
(1) a² + 2ab + b² = (a + b)²
(2) a² - 2ab + b² = (a - b)²
- 합.차의 곱을 이용
(1) a² - b² = (a + b)(a - b)
- x²의 계수가 1 일 때
(1) x² + (a+b)x + ab = (x+a)(x+b)
- 곱하여 상수항이 되는 두 수를 모두 찾는다.
- 위에서 찾은 두 수 중 그 합이 x의 계수가 되는 두 수 a,b를 찾는다.
- (x+a)(x+b) 꼴로 인수분해
- x² 의 계수가 1이 아닌 이차식의 인수분해
(1) acx² + (ad + bc)x + bd = (ac + b)(cx + d)
- 곱해서 x²의 계수가 되는 두 수를 찾는다.
- 곱해서 상수항이 되는 두 수를 찾는다.
- 위에서 찾은 두 수 중 대각선으로 곱하여 x의 계수가 되는 수 a, b, c, d를 찾는다.
- (ac + b)(cx + d)의 꼴로 인수분해
4. 복잡한 식의 인수분해
1) 공통인수가 있으면 공통인수로 묶어내고 인수분해 공식을 이용한다.
2) 공통 부분을 한 문자로 치환하고 인수분해 공식을 이용한다.
3) 항이 여러 개이면 적당한 항끼리 묶어 인수분해한다.
4) 문자가 여러 개 있으면 한 문자에 대하여 내림차순으로 정리한 후 인수분해한다.
5. 이차방정식의 뜻
- x 에 관한 이차방정식 : 방정식의 우변의 모든 항을 좌변으로 이항하여 정리한 식이 (x에 관한 이차식) = 0 꼴로 나타내는 것
- 이차방정식의 일반형 : ax² + bx + c = 0 (a != 0, a, b, c는 상수)
6. 이차방정식의 해
- 해 또는 근 : 이차방정식 ax² + bx + c = 0 을 참이 되게하는 x의 값
- 이차방정식을 푼다 : 이차방정식의 해를 모두 구하는 것을 이차방정식을 푼다라고 한다
7. 인수분해를 이용한 이차방정식의 풀이
- AB = 0 의 성질 : 두 수 또는 두 식 A, B에 대하여 AB = 0 이면 A = 0 또는 B = 0
- 인수분해를 이용한 이차방정식의 풀이
(1) 주어진 이차방정식을 ax² + bx + c = 0 의 꼴로 정리
(2) 좌변을 인수분해한다.
(3) AB = 0의 성질을 이용하여 해를 구한다
8. 이차방정식의 중근
- 이차방정식의 중근 : 이차방정식의 두 근이 중복되어 서로 같을 때, 이 근을 중근이라고 한다.
- 중근을 가진 조건 : 이차방정식이 (완전제곱식) = 0 의 꼴로 인수분해되면 중근을 갖는다.
9. 제곱근을 이용한 이차방정식의 풀이
(1) 이차방정식 x² = k (k >= 0)의 해
x = ±√k
(2) 이차방정식 (x + p)² = q (q >= 0)의 해
(x + p)² = q -> x + p = ±√q -> x = -p±√q
10. 완전제곱식을 이용한 이차방정식의 풀이
- 이차방정식 ax² + bx + c = 0 에서 좌변이 인수분해되지 않을 때, (x - p)² = k 의 꼴로 변형해 해를 구한다.
(1) 이차항의 계수로 양변을 나누어 이차항의 계수를 1로 만든다
(2) 상수항을 우면으로 이항한다
(3) 양변에 (x의계수 /2)² 을 더한다
(4) 좌변을 완전제곱식으로 정리한다
(5) 제곱근을 이용하여 방정식을 푼다
11. 근의 공식을 이용한 이차방정식의 풀이
- ax² + bx + c = 0 (a != 0) 의 근의 공식
12. 이차방정식의 근의 개수
- 이차방정식 ax² + bx + c = 0 (a != 0) 의 근의 개수는 b² - 4ac의 부호에 따라 결정된다
(1) b² - 4ac > 0 이면 서로 다른 두 근을 갖는다
(2) b² - 4ac = 0 이면 한 개의 근(중근)을 갖는다
(3) b² - 4ac < 0 이면 근이 없다
13. 복잡한 이차방정식의 풀이
(1) 계수가 분수나 소수이면 양변에 적당한 수를 곱하여 계수를 정수로 고친다.
- 계수가 분수이면 양변에 분모의 최소공배수를 곱한다.
- 계수가 소수이면 양변에 10의 거듭제곱을 곱한다.
(2) 괄호가 있으면 괄호를 풀어 ax² + bx + c = 0 의 꼴로 정리한다.
(3) 공통 부분이 있으면 한 문자로 치환
14. 이차방정식의 근과 계수의 관계
이차방정식 ax² + bx + c = 0 의 두 근을 A, B 라 할 때
(1) 두 근의 합 : A + B = -a/b
(2) 두 근의 곱 : AB = c/a
15. 이차방정식 구하기
(1) 두 근이 A, B 이고 x² 의 계수가 a인 이차방정식
a(x - A)(x - B) = 0 a{x² - (A + B)x + AB} = 0
(2) 중근이 A이고 x²의 계수가 a인 이차방정식
a(x - A)² = 0
(3) 두 근의 합이 m, 두 근의 곱이 n이고 x²의 계수가 a인 이차방정식
a(x² - mx + n) = 0
16. 계수가 유리수인 이차방정식의 근
계수가 유리수인 이차방정식의 한 근이 p + q√m 이면 다른 한 근은 p - q√m 이다
17. 위로 쏘아 올린 물체에 관한 활용
(1) 시간 t에 따른 높이 h 가 h = at² + bt + c 일 때 높이가 p일 때의 시간은 이차방정식 p = at² + bt +c 의 해이다
(2) 쏘아올린 물체의 높이가 p일 때는 물체가 올라갈 때와 내려올 때 두 번이 생김
(3) 물체가 지면에 떨어질 때의 높이는 0이다