1. 일차함수
함수 y = f(x)에서 y가 x에 관한 일차식 y = ax + b(a,b는 상수 a!=0)로 나타내어질 때 이 함수 f를 일차함수라고 한다.
2. 일차함수 y = ax + b (a!=0)의 그래프
1) 평행이동 : 한 도형을 일정한 방향으로 일정한 거리만큼 이동시키는 것
2) 일차함수 y = ax +b(a!=0)의 그래프
일차함수 y = ax +b의 그래프는 일차함수 y = ax의 그래프를 y축 방향으로 b만큼 평행이동한 직선이다.
3. 일차함수 y = ax +b의 그래프의 x절편, y절편
1) x절편 : 함수의 그래프가 x축과 만나는 점의 x좌표
2) y절편 : 함수의 그래프가 y축과 만나는 점의 y좌표
4. 일차함수 y = ax +b의 그래프의 기울기
x의 값의 증가량에 대한 y의 증가량의 비율은 항상 a로 일정하다. 이 a를 그래프의 기울기라고 한다.
- 기울기 = (y의 값의 증가량) / (x의 값의 증가량) = a
5. 일차함수 y = ax +b의 그래프의 성질
일차함수 y = ax +b(a!=0)의 그래프는 기울기가 a이고 y절편이 b인 직선이다.
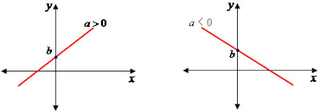
(1) a의 부호에 따른 그래프의 모양 결정
(2) b의 부호에 따른 그래프의 위치 결정
- b > 0 일 때, y축과 양의 부분에서 만난다.
- b < 0 일 때, y축과 음의 부분에서 만난다.
6. 일차함수의 그래프의 평행과 일치
- 두 일차함수의 그래프 y = ax + b, y = a'x + b'
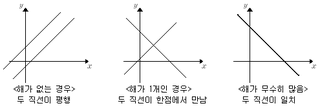
1) 기울기가 같고 y절편이 다른 경우
a = a' , b != b' -> 평행
2) 기울기가 같고 y절편이 같은 경우
a = a' , b = b' -> 일치
- 서로 평행한 두 일차함수의 그래프의 기울기는 서로 같다.
7. 일차함수의 식 구하기
(1) 기울기 a와 y절편을 알 때, 일차함수의 식 구하기
- 기울기가 a이고, y절편이 b인 직선을 그래프로 하는 일차함수 식은 y = ax +b
(2) 기울기 a와 한 점 (x' ,y')를 알 때 일차함수의 식 구하기
- 일차함수의 식을 y = ax +b 로 놓고 , a의 값을 대입
- x = x', y = y'을 대입하여 b의 값을 구한다.
(3) 두 접의 좌표를 알 때 일차함수의 식 구하기
- 기울기공식을 이용해 기울기를 구한다.
- y = ax +b에 기울기 대입
- 두 저중 한 점의 좌표를 대입해 b의 값을 구한다.
(4) x절편과 y절편을 알 때, 일차함수의 식 구하기
- x 절편이 a, y 절편이 b인 직선을 그래프로 하는 일차함수의 식은 두 점 (a,0),(0,b)를 지나고 y절편이 b라는 것을 이용해 구한다
8. 일차함수와 일차방정식의 관계
- 일차방정식 ax + by + c = 0(a, b, c는 상수, a!=0,b!=0)의 해를 나타내는 그래프는
일차함수 y = -a/b x - c/b의 그래프와 같은 직선 이다.
9. 좌표축에 평행한(수직인) 직선
1) 방정식 x = a의 그래프
2) 방정식 y = b의 그래프
10. 연립방정식의 해와 일차함수의 그래프 사이의 관계
연립방정식의 해가 x = p, y = q이면 두 방정식의 그래프, 일차함수의 그래프의 교점의 좌표는 (p,q)이다.
11. 연립방정식의 해의 개수와 두 그래프의 위치 관계
연립방정식의 해의 개수는 두 방정식의 그래프의 교점의 개수와 같다.