정수와 유리수
1. 정수
- 부호를 가진 수 : 서로 반대되는 성질을 가진 두 수량을 나타낼 때 기준을 중심으로 한 쪽은 + 다른 한 쪽은 - 를 붙여 나타냄
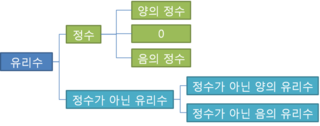
- 정수: 양의 정수, 0, 음의 정수를 통틀어 정수라고 한다.
( 0은 양의 정수도 음의 정수도 아니다.)
2. 유리수
- 양의 유리수, 0 ,음의 유리수를 통틀어 유리수라고한다.
3. 절댓값
- 수직선 위에서 원점과 어떤 수를 나타내는 점 사이의 거리
- 절댓값의 성질
1) 절댓값은 항상 0 또는 양수이다.
2) 0의 절댓값은 0이다.
3) 절댓값이 a(a>0)인 수는 +a, -a 두개이다.
4) 원점에서 멀수록 절댓값이 크다
4. 수의 대소 관계
- 양수는 0보다 크고, 음수는 0보다 작다
- 양수끼리는 절댓값이 클수록 크다.
- 음수끼리는 절댓값이 클수록 작다.
5. 정수와 유리수의 덧셈
- 부호가 같을 때 : 두 수의 절댓값의 합에 공통인 부호를 붙인다.
(+4) + (+2) = +6 , (-4) + (-2) = - 6
- 부호가 다를 때 : 두 수의 절댓값의 차에 절댓값이 큰 수의 부호를 붙인다.
(+4) + (-2) = + 2 , (-4) + (+2) = - 2
6. 정수와 유리수의 뺄샘
- 두 수의 뺄셈은 빼는 수의 부호를 바꾸어 덧셈으로 고쳐 계산
(+5) - (+3) = 5 - 3 = 2
(+5) - (-3) = 5 + 3 = 8
7. 덧셈의 계산 법칙
- 덧셈의 교환법칙 : a + b = b + a
- 덧셈의 결합법칙 : (a + b) + c = a + (b + c)
8. 정수와 유리수의 곱셈
- 부호가 같은 두 수의 곱셈 : 두 수의 절댓값의 곱에 양의 부호를 붙인다.
- 부호가 다른 두 수의 곱셈 : 두 수의 절댓값의 곱에 음의 부호를 붙인다.
9. 곱셈의 계산 법칙
- 곱셈의 교환법칙 : a*b = b*a
- 곱셈의 결합법칙 : (a*b)*c = a*(b*c)
10. 세 개 이상의 유리수의 곱셈
- 음수가 짝수개이면 +, 음수가 홀수개이면 - 를 붙인다.
11. 거듭제곱의 계산
- 양수의 거듭제곱 : 지수에 관계없이 부호는 항상 + 이다.
- 음수의 거듭제곱 : 지수가 짝수이면 + , 지수가 홀수이면 - 이다.
12. 정수와 유리수의 나눗셈
- 부호가 같은 두 수의 나눗셈 : 두 수의 절댓값의 나눗셈의 몫에 양의 부호를 붙인다.
- 부호가 다른 두 수의 나눗셈 : 두 수의 절댓값의 나눗셈의 몫에 음의 부호를 붙인다.
13. 역수를 이용한 나눗셈
- 역수 : 두 수의 곱이 1이 될 때, 한 수를 다른 수의 역수라고 한다.
- 유리수의 나눗셈 : 유리수의 나눗셈은 역수를 이용하여 곱셈으로 바꾸어 계산한다.
14. 유리수의 곱셈과 나눗셈의 혼합 계산
- 나눗셈은 모두 역수를 이요하여 곱셈으로 바꿔 계산.
- 거듭제곱이 있으면 거듭제곱 먼거 계산.
- 곱의 부호를 결성, 각 수의 절댓값의 곱에 부호 붙인다
15. 덧셈, 뺄셈, 곱셈, 나눗셈의 혼합 계산
- 덧셈, 뺄셈, 곱셈, 나눗셈의 혼합 계산
1) 거듭제곰이 있으면 먼저 계산.
2) 괄호가 있으면 괄호 안을 먼저 계산한다.
3) 곱셈과 나눗셈을 먼저 계산하고, 덧셈과 뺄셈은 나중에 계산한다.
- 분배법칙
1) a * (b + c) = b*a + c*a
2) (a + b)*c = a*c + b*c