수학
제곱근과 실수
Happy_Dobi
2016. 11. 1. 16:19
1. 제곱근의 뜻
- 음이 아닌 수 a에 대하여 제곱해서 a가 되는 수를 a의 제곱근이라 한다.
x² = a (a >=0) 일 때 x 를 a의 제곱근이라 한다.
1) 양수의 제곱근은 양수, 음수 두개 이고 두 수의 절댓값은 서로 같다.
2) 0의 제곱근은 0 하나 뿐인다.
3) 제곱하여 음수가 되는 수는 없으므로 음수의 제곱근은 없다.
2. 제곱근의 표현
- 제곱근은 √ 를 사용하여 나타내고 '제곱근' 또는 '루트'라고 읽는다.
- 양수 a의 제곱근 중 양수인 것을 양의 제곱근(√a), 음수인 것을 음의 제곱근 (-√a)라 한다.
3. 제곱은의 성질
a > 0일 때
1) a의 제곱근을 제곱하면 a가 된다.
(√a)² = a, (-√a)² = a
2) 근호 안의 수가 어떤 수의 제곱이면 근호를 없앨 수 있다.
√a² = a, √(-a)² = a
3) a >= 0 일 때 √a² = a
4) a < 0 일 때 √a² = -a
4. 제곱수와 그 성질
1) 제곱수 : 1, 4, 9, 16 .. 과 같이 자연수의 제곱인 수
2) 제곱수의 성질 : 제곱수를 소인수분해하면 소인수의 지수가 모두 짝수이다.
3) 근호 안에 제곱수가 있으면 근호를 없애고 자연수로 나타낼 수 있다.
6. 제곱근의 대소 관계
a > 0, b > 0 일 때
1) a < b 이면 √a < √b
2) √a < √b 이면 a < b
3) a < b 이면 -√a > -√b
7. 유리수와 무리수
1) 유리수 : 정수/(0이아닌 정수) 의 꼴로 나타낼 수 있는 수이다.
2) 무리수 : 유리수가 아닌 수, 즉 순환하지 않는 무한소수 이다.
8. 실수
1) 실수 : 유리수와 무리수를 통틀어 실수라 한다.
2) 실수의 분류

9. 실수와 수직선
- 서로 다른 두 실수 사이에는 무수히 많은 실수가 있다.
- 모든 실수는 각각 수직선 위의 한 점에 대응한다.
- 수직선은 실수에 대응하는 점들로 완전히 메울 수 있다.
10. 실수의 대소 관계
두 실수 a, b의 대소 관계는 a - b 의 부호로 알 수 있다.
1) a - b > 0 이면 a > b
2) a - b = 0 이면 a = b
3) a - b < 0 이면 a < b
11. 제곱근의 곱셈과 나눗셈
a > 0, b > 0 이고 m, n이 유리수일 때
1) 제곱근의 곱셈
-> √a * √b = √ab
-> m√a * n√b = mn√ab
2) 제곱근의 나눗셈
-> √a / √b = √a/b
-> m√a / n√b = m/n√a/b
12. 근호가 있는 식의 변형
a > 0, b > 0 일 때
-> √a²b = √a * √b = a√b
-> √a/b² = √a/√b² = √a/b
13. 분모의 유리화
부모에 유리수가 있을 때, 분모와 분자에 0이 아닌 같은 수를 곱하여 분모를 유리수로 고치는 것을 분모의 유리화라 한다.
14. 제곱근의 덧셈과 뺄셈
m, n 이 유리수이고 a > 0 일 때
1) m√a + n√a = (m+n)√a
2) m√a - n√a = (m-n)√a
15. 근호를 포함한 복잡한 식의 계산
a > 0, b > 0, c >0 일 때
1) 괄호가 있는 경우에는 분배법칙을 이용한다.
-> √a(√b ± √c) = √a√b ± √a√c = √ab ± √ac (복부호 동순)
-> (√a + √b)√c = √a√c ± √b√c = √ac ± √bc (복부호 동순)
2) 분모에 무리수가 있는 경우에는 분모를 유리화한다.
3) 사칙연산이 섞여 있는 경우에는 곱셈과 나눗셈을 먼저 계산한 후 덧셈과 뺄셈을 계산한다.
16. 곱셈 공식을 이용한 근호를 포함한 식의 계산
곱셈 공식을 이용하여 다항식의 곱셈과 같은 방법으로 전개하여 계산한다.
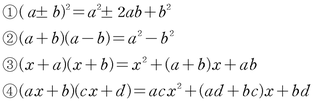
17. 곱셈 공식을 이용한 분모의 유리화
분모가 두 개의 항으로 되어 있는 무리수일 때, 곱셈 공식 (a + b)(a - b) = a² - b²을 이용하여 분모를 유리화한다.